A Concise Overview of Multivariable Calculus
August 24, 2018 - November 23, 2018
A Note to the Reader: I made this guide for myself, with the hope that writing it would not only be a beneficial exercise in organizing my thoughts, but also that it would prove a useful reference in the future. I was also prompted by what I see as a shortage in concise, well-formatted, and easily-readable online math textbooks. Please note that I am not particularly qualified to write on this subject, only recently having taken the course (Math 53 at UC Berkeley). This overview may contain serious errors! Proceed with caution.
Multivariable Calculus, is a very natural extension of single variable calculus. Whereas single variable calculus is concerned with finding derivatives and integrals of single variable functions, multivariable calculus extends these operations to functions of multiple variables. Single variable functions, of course, are functions which take as input a single real number, and which output a single real number, efficiently notated like so:
$$ f: \RR \mapsto \RR $$
Multivariable calculus generalizes the central ideas of single variable calculus to a more intersting (and in many ways more useful) class of functions: those which can be input, and which can output, more than one number, i.e:
$$ f: \RR \mapsto \RR^n $$
$$ f: \RR^n \mapsto \RR $$
$$ f: \RR^n \mapsto \RR^n $$
Functions which take as input a single number, and which output multiple are called vector functions. Functions which take as input multiple numbers, and which output a single, are called multivariable functions, and functions which take as input multiple, such as n, variables and which output the same number, n, numbers are called vector fields. This overview is thus organized into three sections, each exploring how calculus is performed on each class of function.
Table of Contents
Vector Functions
Vector Functions, or vector-valued functions, are functions which output a vector. A vector is a special type of object which has two great properties: vectors can be added, and vectors can be scaled. Formally, a vector in an element of a set called a vector space, which has a precisely defined set of properties. Properties include: addition is commutative and associative, has an additive identity, scalar multiplication is associative and distributive, and has a multiplicative identity.
For our purposes, however, we will only be concerned with vectors which are points in space, and as such can be represented by a list of real numbers -- the coordinates of that point. If a vector $ r $ lives in n-dimensional space, we say that $ r \in \RR^n $. Let $ r_i $ be the ith coordinate of $ r $. This guide will use angle bracket notation to denote particular vectors in $ \RR^n $, for instance:
$$ \langle 1, 2.5, 42 \rangle \in \RR^3 $$
If the above vector is called $ r $, then $ r_1 = 1 $ and $ r_3 = 42 $.
Addition and scalar multiplication are easy to define on these vectors. To add two vectors in $ \RR^n $, simply add the components of each vector. To multiply by a scalar (a real number), simply multiply each component by the scalar. These rules can be stated as:
$$ \forall r, s \in \RR^n: \ (r + s)_i = r_i + s_i $$
$$ \forall r \in \RR^n, \ c \in \RR: \ (cr)_i = cr_i $$
Since addition and multiplication on real numbers is commutative, associative, etc., this definition of addition and scalar multiplication very naturally forces vectors in $ \RR^n $ to satisfy the properties of the vector space axioms (linked above).
Although we can add vectors together, and multiply them by real numbers, defining multiplication between vectors is a little tricky. Think about it -- does it make sense to multiply two points in space together? Is there an intuitive geometric answer to this question? I can't think of one. While it is possible to invent a variety of ways to do this, such as simply multiplying the coordinates together, i.e. $ (rs)_i = r_is_i $, called the Hadamard Product, this doesn't turn out to be a very intereting thing to do.
There are, however, two very useful and interesting operations, reminiscent of multiplication, that we can define between vectors. To discover these, consider the two most natural types of values that we might want multiplying two vectors together to produce. For two vectors in $ \RR^n $, obvious answers would be either a single real number (an element of $ \RR $), or a vector in the same space (an element of $ \RR^n $).
To satisfy these requirements, we define the dot product and the cross product respectively. The dot product of two vectors results in a scalar. The cross product of two vectors results in a vector. In many ways, the scalar result of the dot product and the vector result of the cross product are the most useful and obvious ways of defining such such operations, although that may not be immediately clear.
Define the dot product of two vectors, $ r, s \in \RR^n $ to be:
$$ r \cdot s = \sum_{i=i}^n r_is_i $$
In other words, multiply the components of each vector together and sum over these products. From this definition, we can see that the dot product has the following properties:
The dot product has the following properties:
$$ r \cdot s = s \cdot r $$
$$ r \cdot (s + t) = (r \cdot s) + (r \cdot t) $$
$$ (c_1r) \cdot (c_2s) = c_1c_2(r \cdot s) $$
(Where $ c_1 $ and $ c_2 $ are scalars). The dot product has another useful identity:
$$ r \cdot s = |r||s|\cos\theta $$
To understand the $ \theta $ here, imagine for each vector, $ r $ and $ s $, an arrow emanating from the origin and terminating at each vector's point in space. $ \theta $ then is the angle between these two lines. $ |r| $ denotes the magnitude of vector $ r $, and likewise for vector $ s $. Also note that if two vectors are orthogonal, their dot product will be zero (from $ s \cdot r = |r||s|\cos\theta $ ). An essential intuitive picture of the dot product is that it multiplies the magnitude of one vector by the length of the projection of the other vector onto the first vector. In other words, it is the magnitude of one vector multiplied by the distance that the other vector extends in the direction of the first:
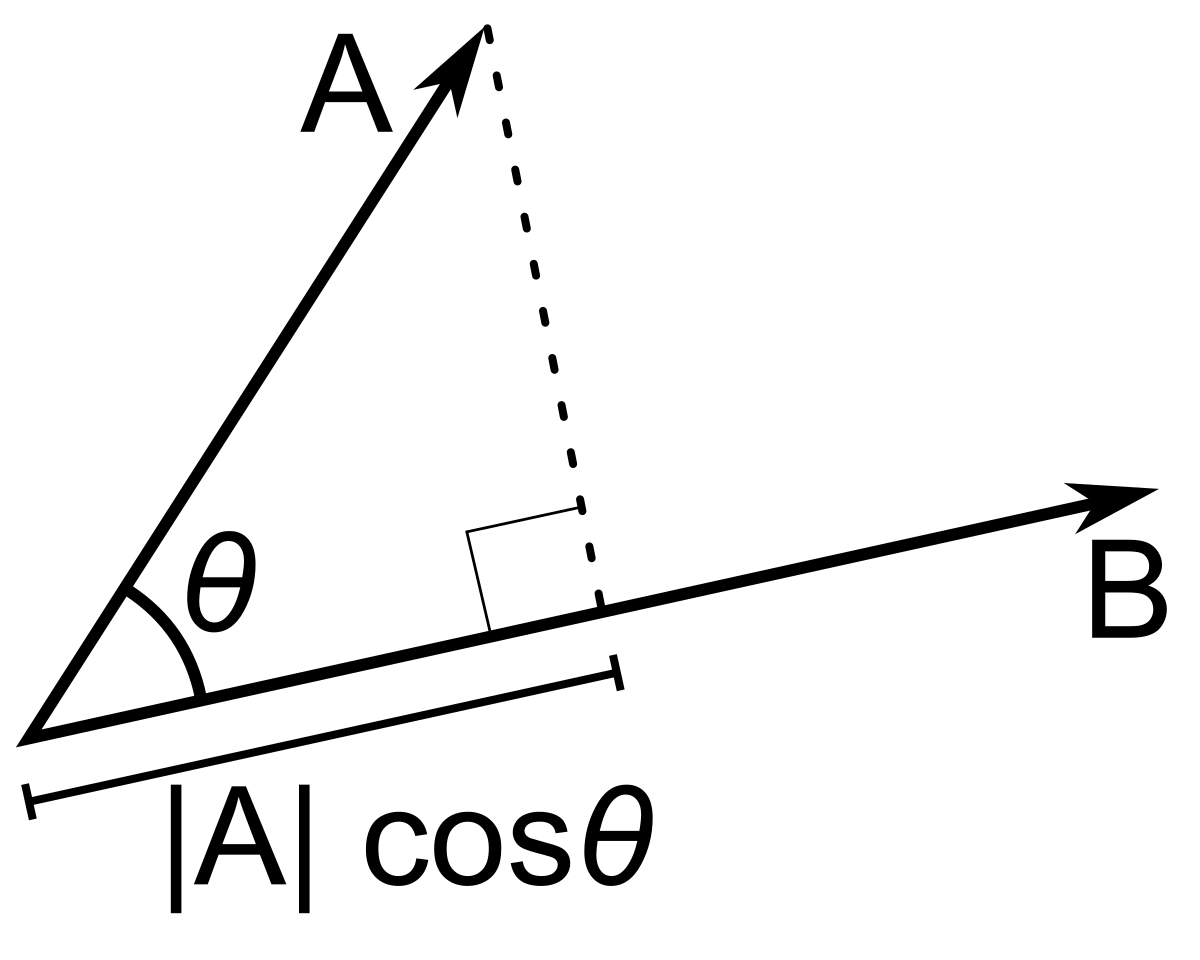
To demonstrate the equivalence of these two formulas for the dot product, note that, from the Euclidean distance formula, $ r \cdot r = |r|^2 $. From the law of cosines (and using the vector names from the above diagram), we know that:
$$ -2|a||b|\cos\theta = |a - b|^2 - |a|^2 - |b|^2 $$
The right hand of which becomes:
$$ (a - b) \cdot (a - b) - (a \cdot a) - (b \cdot b) $$
$ (a - b) \cdot (a - b) $ can be expanded to $ (a \cdot a) - 2(a \cdot b) + (b \cdot b) $, and so cancelling terms and dividing by $ -2 $ we see that $ |a||b|\cos\theta = a \cdot b $.
Now let us define the cross product. The cross product of two vectors, $ r, s \in \RR^3 $, is:
$$ r \times s = |r||s|\sin\theta \ \hat{n} $$
Where the vector $ \hat{n} $ has magnitude 1 and points in a direction orthogonal to both $ r $ and $ s $, defined by the right hand rule. Note that the cross product is only defined this way in 3-dimensional space: $ \RR^3 $. Note that the cross product is $ \vec{0} $ when vectors $ r $ and $ s $ are parallel.

As the diagram indicates, the magnitude of the cross product is equal to the area of the parallelogram defined by the two vectors. This relationship between $ |a \times b| $ and the area of this parallelogram will play an essential role in later integral formulas for the surface area of objects embedded in $ \RR^3 $. The cross product is also given by the following determinant:
$$
r \times s =
\left| \begin{array}{ccc}
\hat{x} & \hat{y} & \hat{z} \\
r_1 & r_2 & r_3 \\
s_1 & s_2 & s_3 \end{array} \right|
$$
Now we are ready to discuss the derivatives of vector functions. Let's first consider vector functions which are of a single variable ($ \RR \to \RR^n $). The output of these functions can be thought of as tracing out a curve in space. Vector functions are especially useful for representing the trajectory of an object through space (where time is the input variable). At each real-numbered location in time, $ t $, the function outputs a vector, $ \vec{r}(t) $ the object's position at that time.

Notice here that we have one quantity, $ \vec{r}(t) $, which depends on another quantity $ t $. Derivatives capture the rate at which one quantity changes with respect to another. In single variable calculus, we had:
$$ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} $$
Very naturally, for vector-valued functions, we now have:
$$ \vec{r}'(t) = \lim_{\Delta t \to 0} \frac{\vec{r}(t + \Delta t) - \vec{r}(t)}{\Delta t} $$
This works because addition and scalar multiplication (subtraction and division) are perfectly well-defined between vectors! Taking the derivative of a vector function generates a new vector function, whose value at each point $ t $ represents the rate at which the vector-valued output changes at that input point.
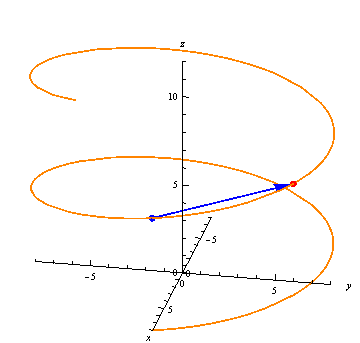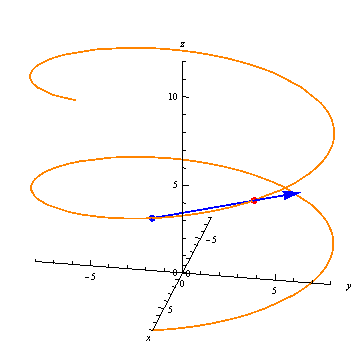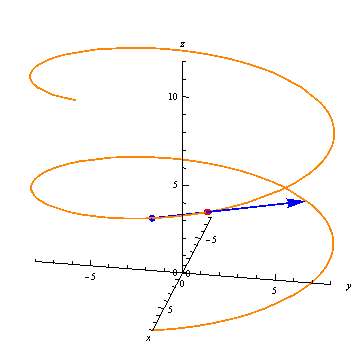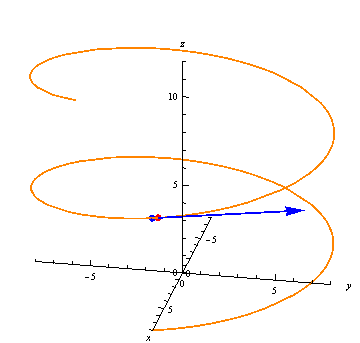
The derivative points from where the function is valued at at some time $ t $, to where it is valued at a lightly later time. If the function represents a trajectory, the derivative is the velocity, and points in the direction of motion.
Let us now consider the components of a vector function: $ \RR \to \RR^n $
$$ \vec{r}(t) = \langle r_1(t), r_2(t) \ ... \ r_n(t) \rangle $$
By the rules of vector addition, and scalar multiplication, we can rewrite our derivative formula as such:
$$ \vec{r}'(t) = \lim_{\Delta t \to 0} \langle \ ... \ \frac{r_n(t + \Delta t) - r_n(t)}{\Delta t} \rangle $$
Which collapses down to:
$$ \vec{r}'(t) = \langle r_1'(t), r_2'(t) \ ... \ r_n'(t) \rangle $$
And thus the derivative of a vector function consists simply of the derivatives of its scalar-valued components. If any one of these derivatives doesn't exist at some point, the derivative of the whole vector function doesn't exist at that point. This arises most naturally when there is some discontinous jump in the curve traced out by the function. A couple additional remarks: (1) since differentiating a vector function yields a vector function, higher derivatives can be taken as expected. (2) Since differentiation is performed component-wise, anti-differentiation is also component-wise.
It is now very natural to ask what other calculus-esque operations we can perform on vector functions. One good one is to find arc length. To find the arc length of a curve, specified by some vector function $ \vec{r}(t) $, between two input values of $ t $, say $ a $ and $ b $, sum up a series of lengths of straight lines connecting nearby points on the curve within the region. Particularly, take the limit as the distance between the points, and the number of lines between them, grows artibrarily large:

At some point $ t $, the infinetesimal unit of length ($ s $) is given by
$$ ds = |\vec{r}'(t)| \ dt $$
Accordingly:
$$ s = \int_a^b |\vec{r}'(t)| \ dt $$
Multivariable Functions
Multivariable Functions are functions of multiple variables. They accept some number of real numbers and output a single real number ($ \RR^n \to \RR $). The easiest class of of them to visualize are functions of the form: $ \RR^2 \to \RR $, as they form a surface 3-d space like so:

Where $ x $ and $ y $ are the input variables and at each corresponding point in the xy-plane, the function outputs a real number on the z-axis. This forms a surface of points in $ \RR^3 $. We now want to extend notions of limits, continuity, differentiation, and integration to such functions. For each of these, the generalization from single variable calculus is quite intuitive.
For functions $ f(x) : \RR^n \to \RR $, and $ a \in \RR^n $, $ \lim_{x \to a} f(x) = L $ if and only if:
$$ \forall \delta \in \RR^+, \ \exists \epsilon \in \RR^+ \ \text{s.t:} $$
$$ |x - a| < \epsilon \implies |f(x) - f(a)| < \delta $$
Intuitively, this means that we can make $ f(x) $ arbitrarily close to $ L $ if we make $ x $ artibrarily close to $ a $.
For single variable functions, a function was continuous at some point $ a $ if:
$$ \lim_{x \to a} f(x) = f(a) $$
Which means the function maps input values $ x $, nearby $ a $ on both the left and the right, to values close to $ f(a) $. The convenient thing here about single variable calclus is that you can only approach a point in the input space ($ \RR $) from two sides -- from values less than $ a $ and greater than $ a $. For multivariable functions, the definition of continuity is the same, but we need to be careful about what a limit means in $ \RR^n $. A multivariable function $ \RR^n \to \RR $ is continuous at a point $ a \in \RR^n $, if and only if:
$$ \lim_{x \to a} f(x) = f(a) $$
But this time, the $ f(x) $ must approach $ f(a) $ no matter what direction $ x $ approaches $ a $ from. This is equivalent to saying that you can make $ f(x) $ as close as you want to $ f(a) $ by choosing some distance $ \epsilon $, such that all $ x $ within a distance $ \epsilon $ of $ a $ map to values within some small distance of $ f(a) $. Stated formally, a function $ f(x) $ is continuous at some point $ a \in \RR^n $ if and only if:
Essential to the definition is a distance function is defined between points in the input space. For $ \RR^n $, the euclidian distance formula is obviously appropriate.